Quote of the Day:
"We think in generalities, but we live in details."
   -- Alfred North Whitehead

Objectives:
The student will determine the area under a curve by 
   summing up rectangles.

1. Collect Homework.

2. Today, we will find areas under curves (i.e., between 
   the curve and the x-axis).  We will sum up the areas of 
   rectangles which approximate the area under the curve.
   We will use several different techniques:
     (1) Using the left-hand endpoints   
     (2) Using the right-hand endpoints     
     (3) Using inscribed rectangles     
     (4) Using the circumscribed rectangles

   The figure below shows how to compute the area under the 
   curve by using the left-hand endpoints.

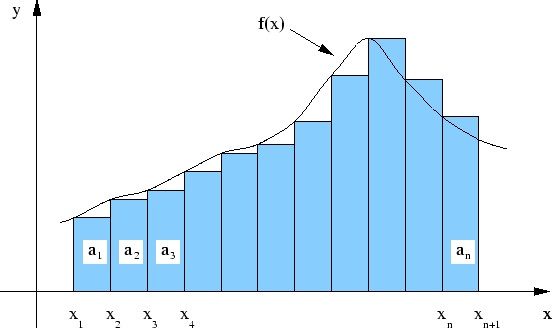
  What happens as we increase the number of rectangles?

3. Example: 
   Determine the area under the curve y = x + 1 on the 
   interval [0, 2] in three different ways:
      (1) Approximate the area by finding areas of
          rectangles where the height of the rectangle is 
          the y-coordinate of the left-hand endpoint
      (2) Approximate the area by finding areas of
          rectangles where the height of the rectangle is 
          the y-coordinate of the right-hand endpoint
      (3) Find the exact area under the curve using 
          geometry   

    #1 Using left hand endpoints and 4 rectangles: 
       (in this example, these are also called 
        inscribed rectangles) 

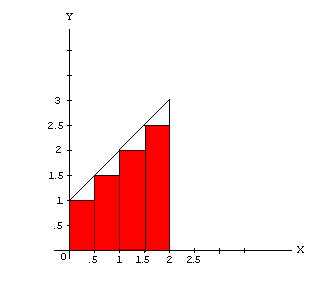
           Area = (.5)(1) + (.5)(1.5) + (.5)(2) + (.5)(2.5)
                =  .5 + .75 + 1 + 1.25 = 3.5 square units
  

    #2 Using right hand endpoints and 4 rectangles: 
       (in this example, these are also circumscribed 
        rectangles) 

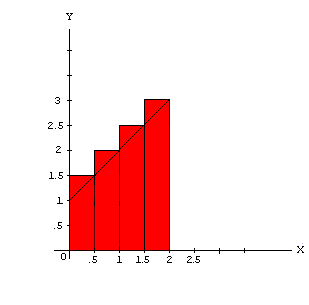
           Area = (.5)(1.5) + (.5)(2) + (.5)(2.5) + (.5)(3)
                = .75 + 1 + 1.25 + 1.5 = 4.5 square units 

        #3 Click here for an interactive link to Riemann Sums (Then click on Integral Machine)
              Click here for another interactive link to Riemann Sums

    #4 Using geometry to find the exact area under the 
       curve:
      
           The figure is a trapezoid, so use the formula 
           for the area of a trapezoid: 

           Area = Average of the Bases x Height  or

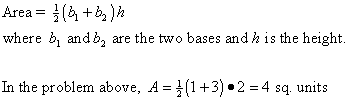
   Note that the average of the first two methods (the
   inscribed and circumscribed rectangles) gives the exact 
   area under the curve.  This only works because the curve 
   is a straight line.  

4. Later in the year, we will use other numerical methods
   to find areas under curves – Simpson's Rule and the 
   Trapezoidal Rule.  Simpson's Rule uses parabolas to 
   approximate the area under the curve and the Trapezoidal 
   Rule uses trapezoids to approximate the area.

   In general, if we wish to determine the area under the 
   following curve,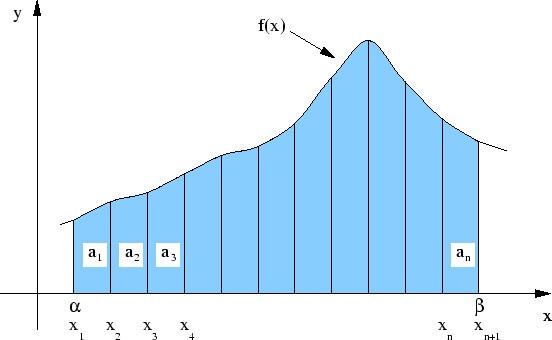

   we could approximate it with rectangles like we did 
   above or we could approximate it with trapezoids like in 
   the diagram below: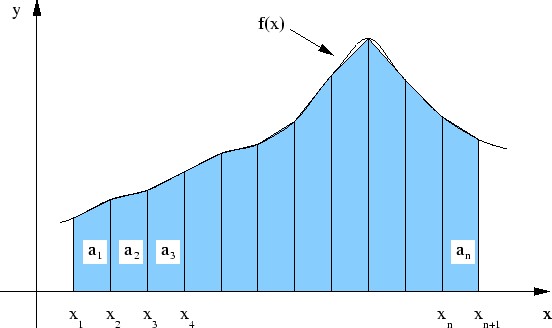

   Notice that the trapezoidal approximation gives a more 
   accurate answer than the rectangular approximation.

   Tomorrow, we will determine the exact area under the 
   curve by increasing the number of rectangles and then 
   applying a limit.

5. Assignment
   Read pages 379-382
   Page 382 (1, 3, 4) use n = 6

Click here to go to the next page