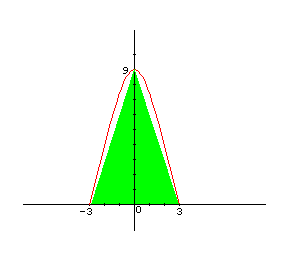
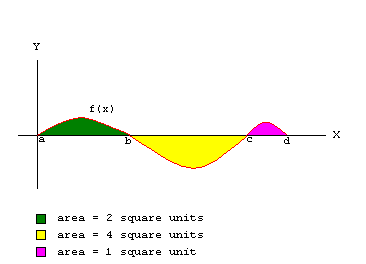
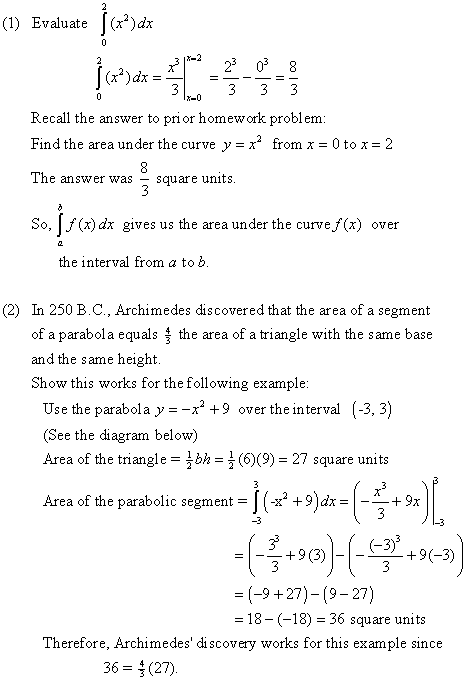Lesson #98 The Definite Integral and Area Under A Curve
|
Quote of the Day:
"But just as much as it is easy to find the differential
[derivative] of a given quantity, so it is difficult to
find the integral of a given differential. Moreover,
sometimes we cannot say with certainty whether the
integral of a given quantity can be found or not."
-- Johann Bernoulli
Objectives:
The student will compute definite integrals.
The student will find the area under a curve by computing
the definite integral.
1. Collect Homework.
2. Definition of the Definite Integral
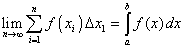
3. Examples
4. Relationship of Area Under a Curve and the Definite
Integral
Given the function above with the areas indicated,
evaluate the integrals below:
5. Show comics with definite integrals
6. Find the area under one arch of the sine curve. 7. Assignment p.414 (17a-d, 19b,c, 20a,b,c, 21) |