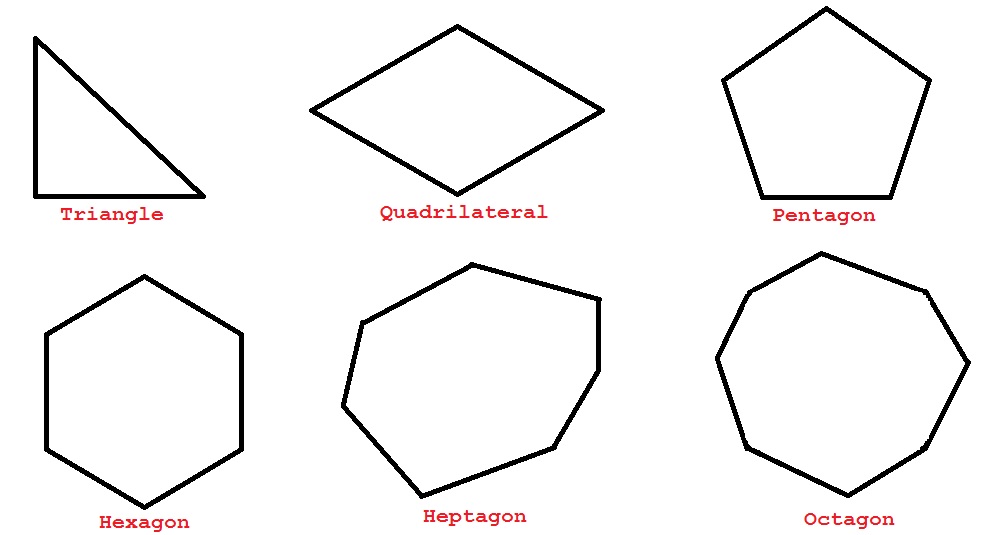
A diagonal of a polygon is a line segment connecting the two vertices that are not endpoints of the same side.
1. Determine the number of diagonals in each of the polygons below and enter your answers in the following table:
| Polygon | Number of Vertices | Number of diagonals from each vertex |
Total number of diagonals |
| Triangle | |||
| Quadrilateral | |||
| Pentagon | |||
| Hexagon | |||
| Heptagon | |||
| Octagon |
2. (A) How many diagonals do you think a polygon with ten sides would have?
(Hint: Do you see any pattern in the table above?)
(B) Draw such a polygon and verify your answer.
3. How many diagonals has a polygon with n sides?
4. Suppose at the end of your class today, each student present shakes hands
just once with every other student.
How many handshakes would be involved?
HINT: First consider some simpler problems:
(A) Suppose there are only four members present.
Represent each member by a vertex of a quadrilateral.
Indicate all possible habdshakes by connecting the appropriate vertices.
How many handshakes are involved?
(B) Use the method above to determine the number of handshakes if
seven students are present.
(C) Do you see any relationship between these solutions and your work with
the polygons in question 1?
(D) Now try to answer the original problem that was posed
(the number of students in your class).
5. How many handshakes would be involved if a class consisted of n members?
6. Here is an interesting game involving vertex connections that you can play
with a friend.
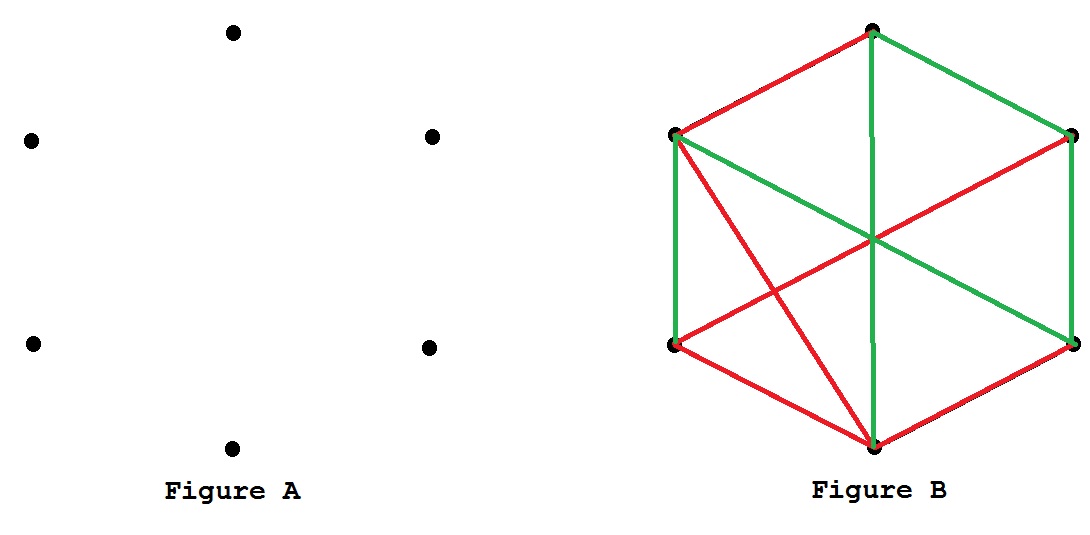
(A) Place six points on a sheet of paper to mark the vertices of a regular
hexagon as shown in Figure A below.
(B) Each player selects a color different from the other.
(C) Take turns connecting pairs of points with line segments.
See Figure B for a partially completed game. Each player has taken 5 turns.
(D) The first player who is forced to form a triangle of his own color
is the loser! (Only triangles whose vertices are among the six
starting points count.)
7. Play this game several times and then answer the questions below.
(A) Is there always a winner?
(B) Which player has the better chance of winning?
8. Use the results of question 7A to help you solve the following problem.
Of any six students in a room, must there be at least three
mutual acquaintances or at least three mutual strangers?
9. Play several more games, but in each case starting with five points that are
the vertices of a regular pentagon, and then answer questions 7A and 7B.