Quote of the Day:
"He who can properly define and divide is to be considered 
   a god."    -- Plato
   
Objectives:
The student will learn another method to evaluate 
   integrals – long division.
  

1. Collect Homework.

2. Definition of the Natural Logarithm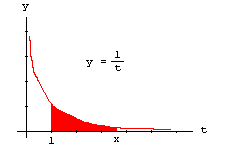

3. Integral formulas for the tangent and cotangent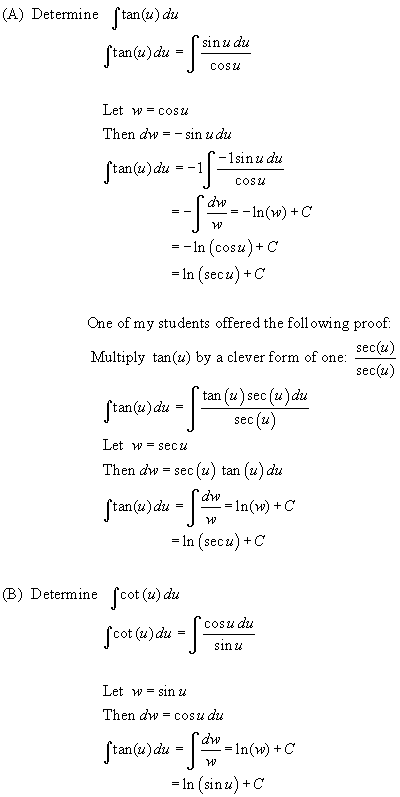

4. Using Long Division to integrate
   First, Show Abbott and Costello's proof that 7x13=28 (Use LONG DIVISION to check)

   If you are trying to integrate a quotient of polynomial 
     expressions, examine the highest powers of the 
     numerator and the denominator.
   If the degree of the numerator is equal to or greater 
     than the degree of the denominator, use long division 
     to simplify the expression.  Then integrate it.

   Examples:

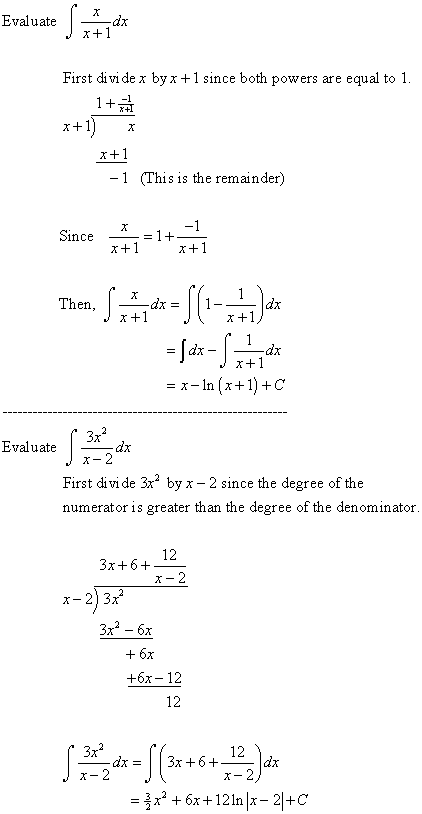
5. Examples: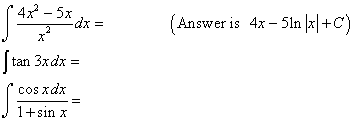

6. Comic strip on Long Division

7. Show the Integral Limerick – work out solution

8. Hand out Find the Bingo Sheets

9. Comic strip on Long Division

10. Comic strip on Long Division

11. Assignment
   p. 451 (3, 7, 31, 32, 33)

Click here to go to the next page