Quote of the Day: 
"Discovery lessons, students writing to learn mathematics,
 the teaching of so-called general problem solving concepts, 
 field trips, math lab lessons, alternate assessments, 
 collaborative partner tests, student presentations, and 
 open-ended problems should all be used sparingly. I use 
 some of them, but they have limited value. Pencil-and-paper 
 analytic solutions are the heart of mathematics education."
   --Michael Stueben in Twenty Years Before the Blackboard

Objectives:
    The student will apply the definition of the derivative 
        to finding derivatives of algebraic functions.
                  
   Given the graph of a function, the student will 
        determine the graph of the derivative.

1. Bellringer.

2. To introduce derivatives:
 

 
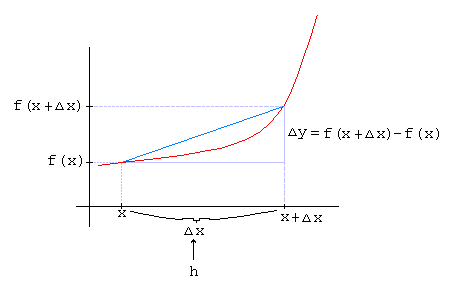
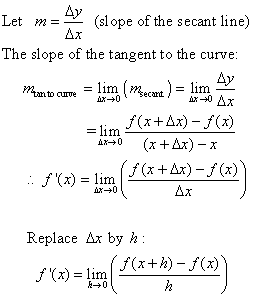
3. Notations for the derivative:

4. Examples:

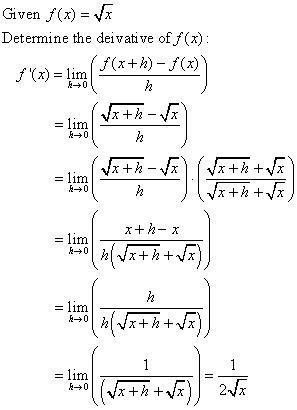
5. Click here for the Derivative Song

6. Comic Strip about the Definition of the Derivative

7. Existence of derivatives:
      The derivative does not exist at any of the 
	following:
 

In the examples above, think of derivative as the slope 
     of the curve at a point.  
In the corner or cusp, the slope cannot be equal to two 
     different values at the same point.
In the vertical tangent, the slope cannot be equal to infinity.
In the point of discontinuity, the slope cannot be equal 
     to two different values at the same x-value.

If f(x) is differentiable,
Then it is also continuous.

The converse of this statement is NOT true:
Continuity does not imply differentiability.


8. Graph of the derivative:

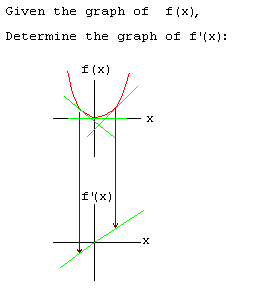
    Click here for an interactive link to the Graph of the Derivative

Use tangents to the graph to approximate the slope 
at various points.  Then graph the values of those 
slopes on an axis below the original function.

9. Assignment:
       p. 187 (5, 7, 9, 11, 15, 21, 23, 25) 

Click here to go to the next page