Quote of the Day:
"If people do not believe that mathematics is simple, it is only
      because they do not realize how complicated life is."

Objectives:
The student will test functions for concavity.
The student will test for points of inflection.

1. Collect homework.

2. Concavity

  A.   concave down – does not hold water
       concave up – does  hold water
     
  B.   Problem:
        A coin is in a "cup" formed by 4 matchsticks.
        Try to get the coin out of the cup by moving only 2 
        matchsticks to new positions to form a "congruent 
        cup" in a new position.

  C.  What is happening to the tangent lines in a graph as you 
      go from left to right?  

         concave up – they are increasing
         concave down – they are decreasing


      The second derivative is a rate of change of the 
      first derivative.

         if f''(x) > 0, then concave up.
         if f''(x) < 0, then concave down.       

      Use Mr. Smiley and Mr. Frowny to help you remember 
      this:  

3. Points of Inflection

   Points of inflection occur when the concavity changes.

   Test:  If there is a point of inflection, the second 
          derivative is zero. 
          BUT just because the second derivative is zero
          doesn't guarantee a point of inflection.

   Draw diagrams on board to illustrate.
   Example where 2nd derivative is zero, but Not a point of 
           inflection:    

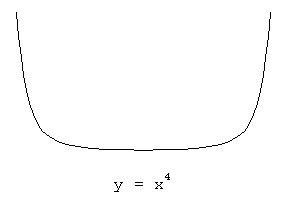
    The Normal Distribution Curve

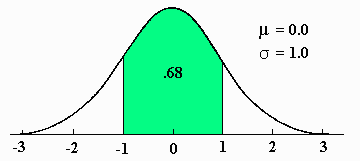
       The point of inflection on the normal 
       curve is where the first standard 
       deviation occurs.

4. To test for points of inflection and concavity:
   (1) Take the second derivative of the function.
   (2) Set it equal to zero and solve for x.
       These values of x are possible points of inflection.  
   (3) Test on either side of these points to check 
       concavity. If the concavity changes from positive to 
       negative or from negative to positive, it is a point 
       of inflection.

5. Example:
    Test the following function for intervals where it 
    increases and decreases, for intervals where it is 
    concave up and concave down, and for points of 
    inflection. 

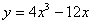
6. Discuss the S-Curve (Handout)

7. Look at comics involving normal curve and concavity 

8. Assignment: 
       p. 276 (9, 11, 13, 15, 16, 29, 35, 36, 37) 

             
         

Click here to go to the next page