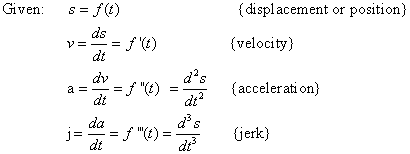|
Quote of the Day:
"The shortest distance between two points is under construction."
-- Bill Sanderson
Objectives:
The student will compute higher order derivatives.
The student will be able to compute velocity and
acceleration for a given displacement function.
1. Collect Homework.
2. Higher-Order Derivatives (Second derivatives, …)
To determine the second derivative, take the
derivative of the first derivative.
The notation for the second derivative:

Examples:

3. Distance, Velocity, and Acceleration
A. Problem:
You make a roundtrip from Winchester to Harrisonburg,
a distance of 60 miles one way (actually, any distance
will work in this problem). If you travel down at
30 m.p.h., and return at 60 m.p.h., what was your
average m.p.h. over the whole trip?
Use the following table to help answer the problem:

B. Problem:
There is a single path up a mountain in Shenandoah
National Park.
A mountaineer starts up at 7:00 AM and arrives at the
top at 7:00 PM. She stays there overnight.
The next morning, she starts back down at 7:00 AM and
arrives at the bottom at 7:00 PM.
On both days, she travels at varying speeds – enjoying
the scenery, stopping for lunch, smelling the roses…
What is the probability that there was a spot on the
trail that she passed at exactly the same time on both
days?
Hint: Draw a Displacement – Time graph!
Answer: It is 100%. Look at the Displacement-Time
Graph – it doesn't matter how long she takes to come
back down, there must be at least one place where the
descent curve must cross the ascent curve.

C. Given a displacement curve, s = f(t)
The velocity is defined to be the change in the
displacement divided by the change in time,
or in other words, the first derivative of
displacement with respect to time.
It measures how fast you are going.
The acceleration is defined to be the change in the
velocity divided by the change in time, or in
other words, the derivative of velocity with
respect to time.
When you press down on the accelerator in your
car, you are changing the velocity.
The jerk is a sudden change in acceleration. When
a ride in a car is jerky, it is not that the
accelerations involved are necessarily large but
that the changes in acceleration are abrupt.
Jerk is what spills your soft drink.
The derivative responsible for jerk is the third
derivative of position.
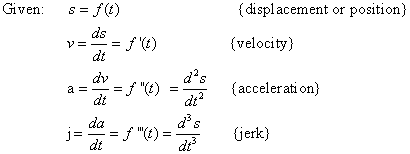
Example:

4. Assignment:
p. 197 (3, 29, 30, 33, 41, 44, 45, 47, 67)
Click here to go to the next page
|