|
Quote of the Day:
"The mathematician's patterns, like the painter's or
poet's, must be beautiful. The ideas, like the colours
or the words, must fit together in a harmonious way.
Beauty is the first test: There is no permanent place in
the world for ugly mathematics.
-- G. H. Hardy
Objectives:
The student will review all concepts related to curve
sketching.
1. Collect homework.
2. Click here for Methods for Finding Critical Points
3. Outline of the test on chapter 5 (No calculators):
#1 Given a function, determine the derivatives, the
relative extrema, points of inflection, intervals
where the function is concave up/down and where
it is increasing/decreasing.
#2-4 Sketch the function which satisfies certain
conditions.
#5-7 Sketch the graphs of given functions, indicating
relative max/min points.
#8 Discussion question about curve sketching.
#9-10. Problems involving curve sketching
(find the value of k…)
4. Review for the test
Sketch the following function, discussing relative
extrema, points of inflection, intervals of concavity
and intervals of increasing/decreasing…
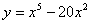
5. Riddle:
Why are huge chrysanthemums like some parabolas?
Answer: Because they're both maximums.
6. Assignment
p. 319 (6)
p. 321 (2, 6)
Study for the Test
Click here to go to the next page
|