Lesson #76 Applied Maximum Minimum Problems
-- Cat Food Can Problem
|
Quote of the Day:
"The only way to learn mathematics is to do mathematics. That tenet is
the foundation of the do-it-yourself, Socratic, or Texas method, ..."
-- Paul Halmos
Objectives:
The student will learn to solve applied maximum minimum problems.
1. Collect homework. Go over some of the Applied Max/Min
Problems.
2. Example #1
Discuss the Cat Food Can Problem (Tin Can Problem).
Letter from Carnation. Read letter from M&M's.
3. Example #2
Determine the largest cone that will fit in a sphere of
radius 6 centimeters.
Solution:
Draw a diagram:
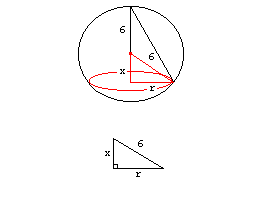
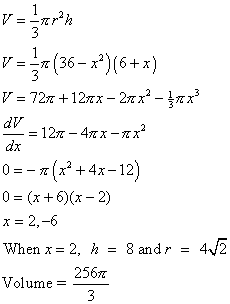
Click here for Poem about Einstein and Sphere and Cone 4. Example #3 A woman in a rowboat at P, 5 miles from A -- the nearest point on shore, wishes to reach B, which is 6 miles from point A in the shortest time. Where should she come ashore if she can row 2 mi/hr and walk 4 mi/hr? 
Solution: Since Time = Distance / Velocity 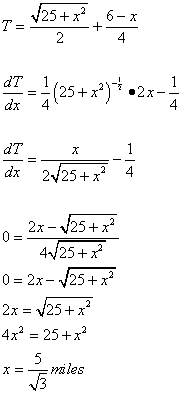
5. "Do Dogs Know Calculus?" (Same type of problem) 6. Assignment: p. 348 (9, 11, 56a, 57, 62) |