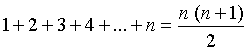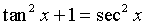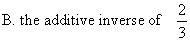Calculus is a study of operations – differentiation and integration – that are performed 
	on functions rather than on numbers.  
	To be well prepared for calculus, you should be thoroughly familiar with the 
		elementary functions.  
	Specifically, you should know the definitions of the various types of functions, 
		recognize their graphs, know their properties, and be able to apply them 
		to both the real world and the mathematical world.  
	This examination is designed to see how well you are prepared.


I. A function is a kind of relation.
	A. Write the definition of a relation.
	B. What special property makes a relation a function?


II. Functions are often defined by a general equation.
     Write the general equation for:
	A. a linear function
	B. a quadratic function
	C. an exponential function
	D. a sinusoidal function


III. Some kinds of functions are defined in other ways.
      Write the definition for:
	A. the inverse of a function
	B. the cosine trigonometric function
	C. a geometric sequence
	D. an arithmetic sequence
	E. an infinite geometric series
	F. a parametric function


IV. The behavior of a function or relation is revealed by its graph.
       Sketch a graph of:
	A. the tangent function
	B. a cubic function
	C. the normal distribution curve
	D. a linear function
	E. the inverse cosine function
	F. the inverse cosine relation
	G. the inverse tangent function
	H. y = sin(3x) + 2
        I. the logaritnic function

V. Different kinds of functions have different properties.  State:
	A. the Pythagorean property for sines and cosines (Trig Identity)
	B. the double angle property for cos(2x) and sin(2x)
	C. the trig identity for sin (A – B)
	D. the trig identity for cos (A + B)
	E. the expansion of the binomial theorem
	F. the identity that involves cosecant and cotangent
	G. the Law of Sines
	H. the area of a triangle using the sine function


VI. Proofs are certainly important in mathematics.
       The development of an idea is certainly far more important than the final result.
        Prove:
	A. the area formula for a triangle using the sine function.

	B. the sum of the positive odd integers from 1 to n is

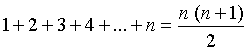
	    using mathematical induction.

	C. that the following is an identity:

 

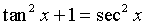
VII. The word "inverse" appears often in mathematics.
        Determine:
	A. the multiplicative inverse of  -88.

 	  
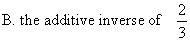
	C. the inverse function of   y = 4x – 7

 
	E. the inverse function of y = ln(x)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -


The following concepts will be used in A.P. Calculus:

I. Algebra
	A. Solving linear equations
	B. Solving quadratic equations
	C. Solving systems of linear and quadratic equations
	D. Solving polynomial equations using the Rational Roots Theorem
	E. Using long division with polynomials
	F. Expanding a binomial using the Binomial Theorem
	G. Applying Pascal's Triangle to binomials
	H. Determining the sum of an infinite geometric series
	I. Determining the equation of a line, given the slope and one point
        J. Simplifying logarithmic and exponential expressions 
        K. Solving logarithmic and exponential equations
  
II. Geometry
	A. Applying the Pythagorean theorem
	B. Finding areas and perimeters of geometric figures
		(trapezoids, rectangles, squares, circles, triangles)
	C. Finding volumes of cubes, cylinders, cones, and spheres
	D. Finding the area of a triangle using Heron's formula

III. Precalculus
	A. Proof by induction
	B. Trig identities
	C. Trig definitions
	D. Solve trig equations
	E. Law of Sines
	F. Law of Cosines
	G. Area of a triangle using the sine function
	H. Graphing trig and inverse trig functions