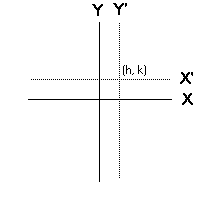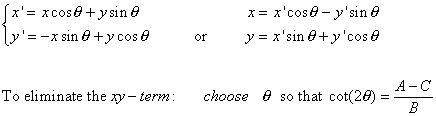I. General Form of the 2nd degree equation in 2 variables:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
A. Test the discriminant B2 - 4AC
|
If B2 - 4AC < 0
|
Then Ellipse, Circle, Point, or Nothing
|
|
If B2 - 4AC > 0
|
Then Hyperbola or Two Intersecting Lines
|
|
If B2 - 4AC = 0
|
Then Parabola, Two Parallel Lines, One Line, or Nothing
|
B. If B = 0, the equation becomes Ax2
+ Cy2 + Dx + Ey + F = 0
|
If A and C are both positive or both negative
|
Then Ellipse, Circle (if A = C), Point, or Nothing
|
|
If A and C are of opposite signs
|
Then Hyperbola or Two Intersecting Lines
|
|
If A = 0 or B = 0
|
Then Parabola, Two Parallel Lines, One Line, or Nothing
|
II. Translations from xy-axes to x'y'-axes
|
|
x' = x - h
y' = y - k
|
or
|
x = x' + h
y = y' + k
|
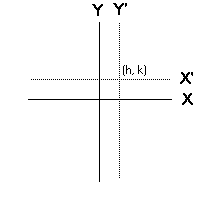
|
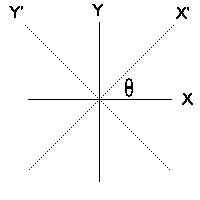
III. Rotations from xy-axes to x'y'-axes
|