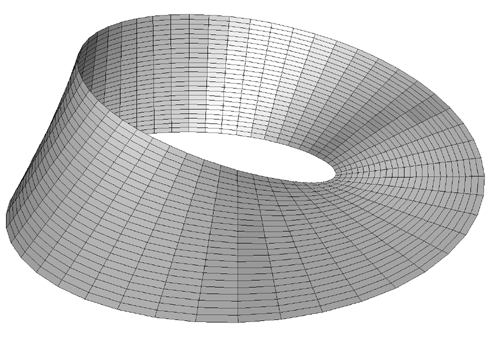
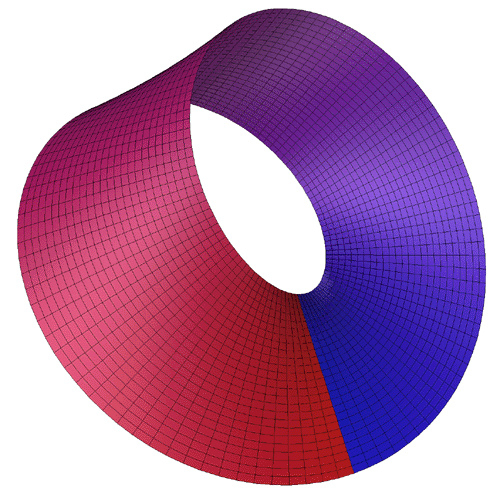
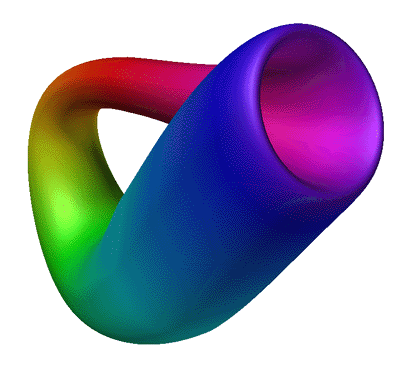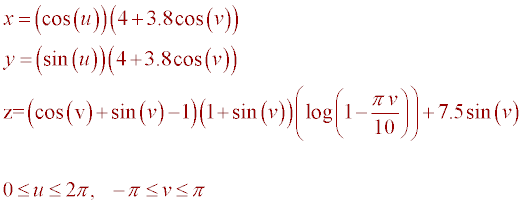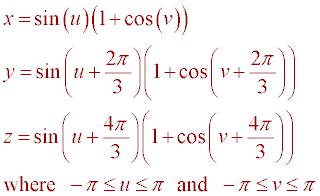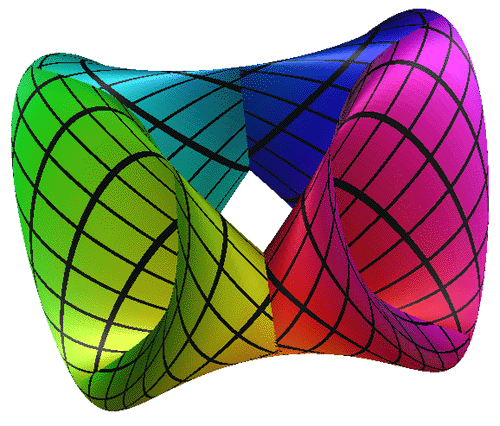Example 1: The Möbius Strip
The Möbius strip is the simplest geometric shape which has only one
surface and only one edge. It can be created by taking a strip of paper,
giving it a half twist along its long axis, and then joining the two narrow
ends together. The Möbius strip in 3 dimensions can be represented
parametrically f(s,t) as follows:

| Paul Bourke |
|
| Paul Bourke |
|
| M.C. Escher |

|
| M.C. Escher |

|
| M.C. Escher |

|
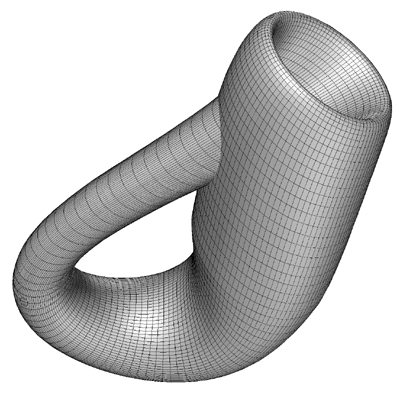
Example 2: The Klein Bottle
Most containers have an inside and an outside, a Klein bottle is a closed surface
with no interior and only one surface. It is not able to be constructed in 3
dimensions without intersecting surfaces. It can be realized in 4 dimensions.
The classical representation is shown below.
The Klein Bottle can be represented parametrically f(u, v) as follows:

| Paul Bourke |
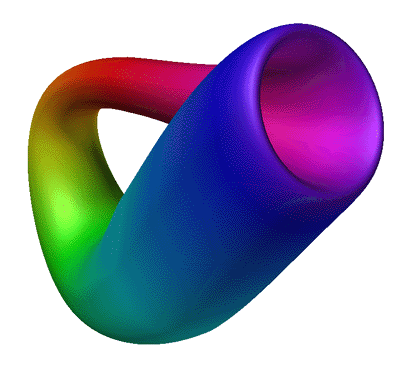
|
| Paul Bourke |
|
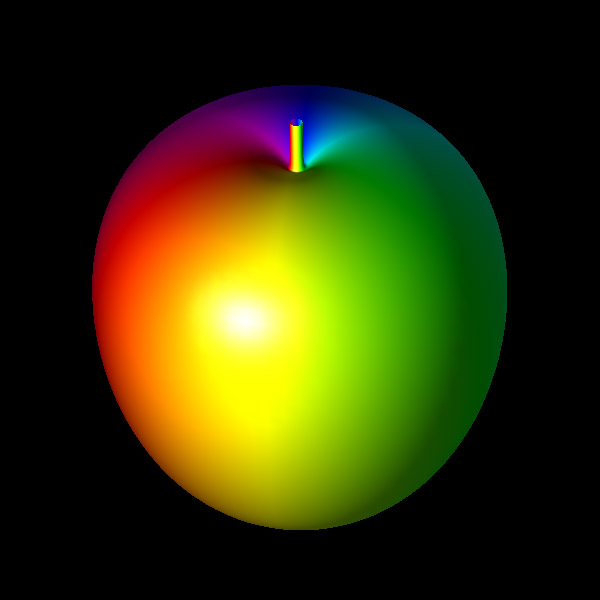
Example 3: Apple
The Apple Surface can be represented
parametrically f(u,v) as follows:
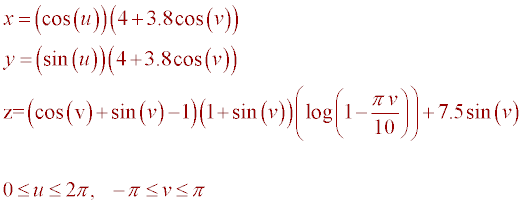
| Paul Bourke |

|
| Paul Bourke |
|
Example 4: The Triaxial Tritorus
The Triaxial Tritorus is defined
parametrically as follows:
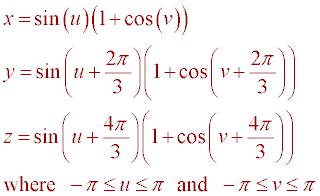
| Paul Bourke |

|
| Paul Bourke |
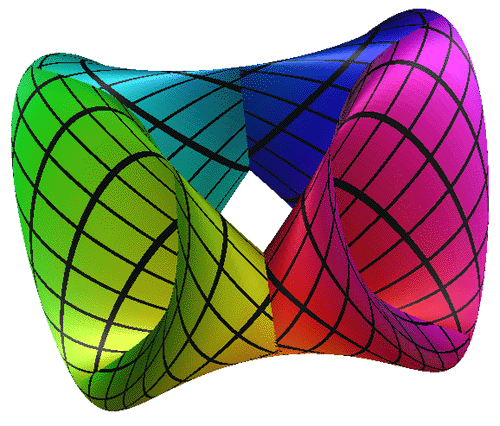
|
| Paul Bourke |

|