What is the probability that in a group of 4 people, at least two are born in the same month?
You may assume that all months have the same probability (which in reality they do not, but we will address that next month!).
Solution to the Problem:
The answer is .4271 or 42.71%.You solve this the same way that you solve the original Birthday Problem.
First, determine the probability that all four people are born in different months:
The first person could be born in any of the 12 months: (12/12)
The second person could be born in any of the 11 months remaining: (11/12)
The third person could be born in any of the 10 remaining months: (10/12)
The fourth person could be born in any of the 9 remaining months: (9/12)
So the probability that all four are born in different months is:
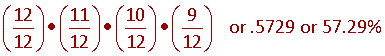
Therefore the probability that at least 2 of them are born in the same month is

James Alarie sent in a different way of solving the problem:
Of the 12 x 12 x 12 x 12 = 20736 possible birthday combinations, 8856 have at least one pair born in the same month. This reduces to 41 of 96 or 42.7%.
Correctly solved by:
| 1. James Alarie | Flint, Michigan |
| 2. Keyan Miller |
Mountain View High School, Mountain View, Wyoming |