Solution to the Problem: The answer is .4271 or 42.71%.
You solve this the same way that you solve the original Birthday Problem.
First, determine the probability that all four people are born in different months:
The first person could be born in any of the 12 months: (12/12)
The second person could be born in any of the 11 months remaining: (11/12)
The third person could be born in any of the 10 remaining months: (10/12)
The fourth person could be born in any of the 9 remaining months: (9/12)
So the probability that all four are born in different months is:
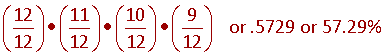
Therefore the probability that at least 2 of them are born in the same month is

James Alarie sent in a different way of solving the problem:
Of the 12 x 12 x 12 x 12 = 20736 possible birthday combinations, 8856 have at least one pair born in the same month. This reduces to 41 of 96 or 42.7%.