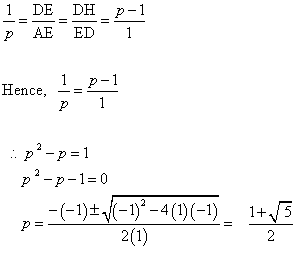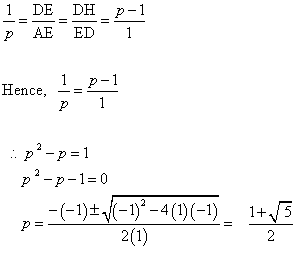In the pentagon shown below, each side of the pentagon is equal to one, that is,
AC = CE = DE = DB = BA = 1.
The five diagonals are drawn to form a pentagram.

What is the perimeter of triangle EFG?
Solution to the Problem:
The perimeter of the triangle is equal to the golden ratio, (1 + sqrt(5)) / 2 or approximately, 1.618.
Let p = perimeter of triangle FGE = GE + EF + FG
Then I showed that p= EG + BH + GH, which is a diagonal of the pentagon.
In rhombus ECAH, AH = EH = EC = AC = 1
Then I focused on triangles DAE and HED.
They share the same base angle ADE.
Also, AD = AE = p and HE = DE = 1.
So the two triangles are similar.
Triangle EAD has sides DA = AE = p and DE = 1.
Triangle DEH has sides ED = EH = 1 and DH = AD – AH = p – 1.
Then since the triangles are similar, you can set up ratios of the sides: