Solution to the Problem: There must be at least thirteen players in the tournament.
Since the last player beat the top three players, he must have a total of three points (3 wins).
Each match results in ONE POINT ( a win/loss or 2 ties).
Use the combinations formula
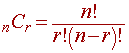to determine the number of points for n players taken r at a time).
Begin with the last person scoring 3 points, then add .5 points to each player in the standings.
For example with 4 players (the very minimum from the given info), there would be 3, 3.5, 4, and 4.5 points as the very minimum. This gives a total of 15 points but only 6 matches (and therefore 6 points) would be played. So, continue to compute each combination and check it with the minimum possible score. The first one to match is n = 13.
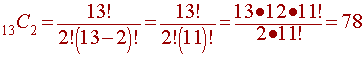
so 13 contestants play 78 matches (and therefore get a total of 78 points).
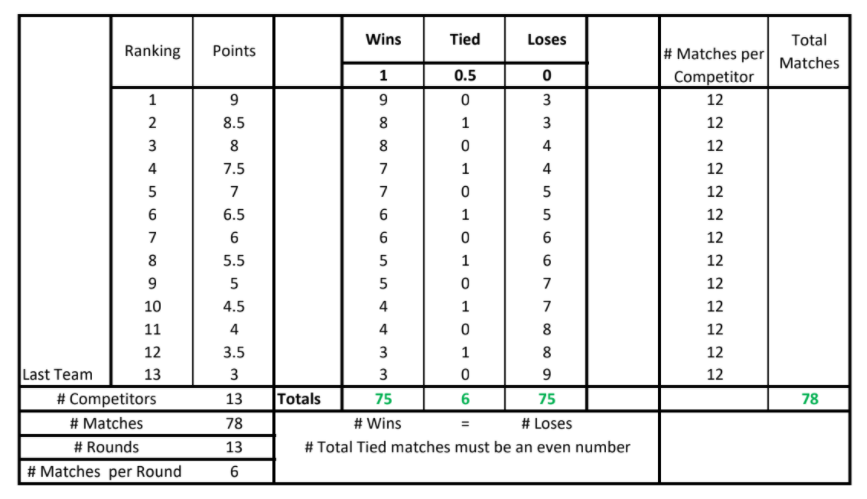
Here are the final scores for the thirteen players: 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 and these add up to 78 points.
Each player has a different score and the last player beat the top three players so he has 3 points.
Below is a table showing all the calculations until I found the one that worked:
| Number of contestants |
Total # of matches (and Total POINTS) |
Smallest possible points |
|---|---|---|
| 4 | 6 | 3 + 3.5 + 4 + 4.5 = 15 (Not Possible because only 6 matches were played) |
| 5 | 10 | 3 + 3.5 + 4 + 4.5 + 5 = 20 (Not Possible because only 10 matches were played) |
| 6 | 15 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 = 25.5 (Not Possible because 15 < 25.5) |
| 7 | 21 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 + 6 = 31.5 (Not Possible because 21 < 31.5) |
| 8 | 28 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 + 6 + 6.5 = 38 (Not Possible because 28 < 38) |
| 9 | 36 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 = 45 (Not Possible because 36 < 45) |
| 10 | 45 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 = 52.5 (Not Possible because 45 < 52.5) |
| 11 | 55 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 = 60.5 (Not Possible because 55 < 60.5) |
| 12 | 66 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 +8.5 = 69 (Not Possible because 66 < 69) |
| 13 | 78 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 +8.5 +9 = 78 (Possible because 78 = 78) |
Colin Bowey sent in the final standings of the participants:
Veena Mg sent in an algebraic solution:
It is a Round Robin format.
If 'n' is number of teams,
number of matches played will be
= n *( n - 1) /2 - - - - - - - (A)
The team who stood last, defeated the first 3 teams. That means, the last team has scored at least 3 points.
For all the teams to have scored different points, there should at least be a minimum difference of 0.5. That means the scores are in an AP with a common difference of 0.5, and starting with 3
Total score of all teams, can at max be equal to number of games played.
The sum of AP is given by formula =
(n/2) * ( 2a + (n-1) *d)) - - - - (B)
a = 3, d = CD = 0.5
(A) should be greater than or equal to (B)
To find minimum number of competitors, equate both of them.
n * (n - 1) /2 = (n/2) * ( 2a + (n-1) *d))
n - 1 = (6 + (n-1)*0.5)
n = 6.5/0.5
n = 13.
So, a minimum of 13 competitors should play, to satisfy the given conditions..