Solution to the Problem: The distance between the centers is 9 meters or 21 meters depending on whether the center of the small circle is in the interior or exterior of the larger circle (see diagrams below).
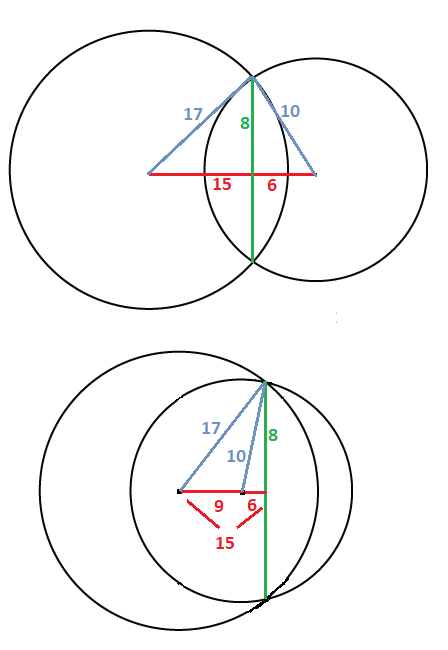
Use the Pythagorean theorem to solve for two right triangles in each diagram.
Consider the first diagram where the center of the smaller circle is in the exterior of the larger circle:
In the first triangle the hypotenuse is 17 and one leg is 8, so the other leg is 15 meters.
In the second triangle the hypotenuse is 10 and one leg is 8, so the other leg is 6 meters.
So, the distance between the two centers is 15 + 6 = 21 meters.
Mow consider the second diagram where the center of the smaller circle is in the interior of the larger circle:
In the first triangle the hypotenuse is 17 and one leg is 8, so the other leg is 15 meters.
In the second triangle the hypotenuse is 10 and one leg is 8, so the other leg is 6 meters.
But this time, the distance between the two centers is 15 - 6 = 9 meters.