My answer for the ten cities is 18 and my extra credit answer is 2000.
Here is a drawing for ten cities and the 18 connections:

This is the smallest number of connections that I could find. You do not need all the diagonals in order to make all the routes between any two cities. A general formula that works is the number of sides of the polygon (or the number of cities) plus the number of diagonals from one vertex, then add one. I developed the formula by drawing pictures for 4 cities, 5 cities, 6 cities, 7 cities, and 8 cities. Then I checked to make sure that I could traverse all the routes between any two cities. Then I generalized the formula. Here is a chart showing my results:
| Cities | n (number of flights) |
|---|---|
| 3 | 3 + 0 = 3 |
| 4 | 4 + 2 = 6 (sides of polygon plus diagonals needed) |
| 5 | 5 + 3 = 8 |
| 6 | 6 + 4 = 10 |
| 7 | 7 + 5 = 12 |
| 8 | 8 + 6 = 14 |
| : | : |
| x | x + (x - 2) = 2x - 2 |
So when x = 10, the number of connections is 2(10) - 2 = 18.
So when x = 1,001 cities, the smallest number of flights needed is 2(1001) -2 = 2000.
Here are my drawings for 5 cities, 6 cities, 7 cities, and 8 cities:
5 Cities

6 Cities

7 Cities
 8 Cities
8 Cities 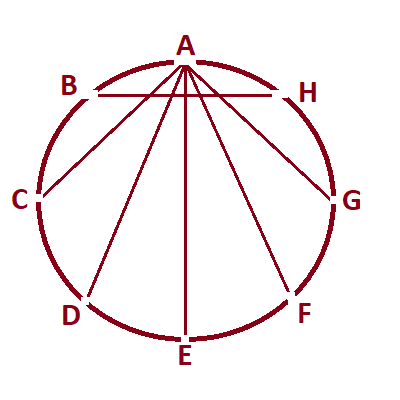
Now, let us examine the minimum number of connections needed for 7 cities. Using the combinations formula, there are 21 combinations of 7 cities, taken two at a time. Listed below are the routes for those 21 combinations. Using the general formula, the number of connections needed is 12 and is shown in the table above and in the diagram above.
Here are the routes:
| Trip # | Trip | Route |
|---|---|---|
| #1 | A - B | A - G - F - E - D - C - B |
| #2 | A - C | A - B - G - F - E - D - C |
| #3 | A - D | A - C - B -G - F - E - D |
| #4 | A - E | A - D - C - B - G - F - E |
| #5 | A - F | A - E - D - C - B - G - F |
| #6 | A - G | A - B - C - D - E - F - G |
| #7 | B - C | B - A - G - F - E - D - C |
| #8 | B - D | B - C - A - G - F - E - D |
| #9 | B - E | B - C - D - A - G - F - E |
| #10 | B - F | B - C - D - E - A - G - F |
| #11 | B - G | B - C - D - E - F - A - G |
| #12 | C - D | C - B - A - G - F - E - D |
| #13 | C - E | C - D - A - B - G - F - E |
| #14 | C - F | C - D - E - A - B - G - F |
| #15 | C - G | C - D - E - F - A - B - G |
| #16 | D - E | D - C - B - A - G - F - E |
| #17 | D - F | D - E - A - C - B - G - F |
| #18 | D - G | D - E - F - A - C - B - G |
| #19 | E - F | E - D - C - B - A - G - F |
| #20 | E - G | E - F - A - D - C - B - G |
| #21 | F - G | F - E - D - C - B - A - G |