If Jonah had driven for 20 minutes less than the time he would have driven if he had driven 20 miles less than he did drive but at two-thirds the speed at which he drove,
he would have driven 10 miles less than he did.
However, if he had driven 20 minutes longer than the time he would have driven if he had driven 10 miles less than he did drive but at three-quarters the speed at which he drove,
he would have driven 20 miles further.
How far, in miles, did Jonah drive?
Solution to the Problem:
Jonah had driven for a distance of 64 miles.
Let D = original mileage.
Let S = original speed
Then you can write equations for the two statements:
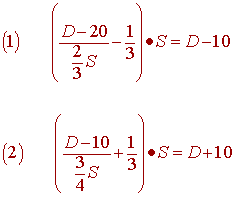
Now solve the two equations simultaneously:
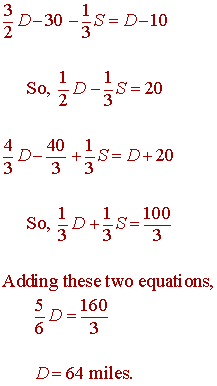
Here is K. Sengupta's solution:
Let d be the actual distance (miles).
Let s be the actual speed (miles/hr).
To get all units in miles and hours, we must use
20 min = 1/3 hr.
From the two given sentences, we can write two equations, keeping in mind that Distance = Rate x Time and Time = Distance / Rate
((d-20)/(2s/3) - 1/3) s = d - 10
and
((d-10)/(3s/4) + 1/3) s = d + 20
From the first:
3s(d-20)/(2s) - s/3 = d - 10
3d/2 - 30 - s/3 = d - 10
9d - 180 - 2s = 6d - 60
3d = 2s + 120
From the second
4s(d - 10)/(3s) + s/3 = d + 20
4d/3 - 40/3 + s/3 = d + 20
4d - 40 + s = 3d + 60
d = 100 - s
3d = 300 - 3s
2s + 120 = 300 - 3s
5s = 180
s = 36
d = 64
Consequently, Jonah had driven for a distance of 64 miles.
Correctly solved by:
| 1. Seth Cohen | Concord, New Hampshire |
| 2. Kelly Stubblefield | Mobile, Alabama |
| 3. Rob Miles | Northbrook, Illinois |