How many ordered triples of integers (a, b, c), with a ≥ 2, b ≥ 1, and c ≥ 0,
satisfy both logab = c2005 and
a + b + c = 2005?
Solution to the Problem:
There are two ordered triples (2004, 1, 0) and (1002, 1002, 1).
[EXPLANATION]:
Use the definition of a logarithm: If logxy = w, then y = xw
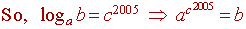
Look at different possibilities for c:
If c = 0, then a0 = b. therefore b = 1.
So, a = 2005 - 1 - 0 = 2004.
So there is one triple: (2004, 1, 0) that satisfies the conditions.
If c = 1, then a1 = b. therefore b = a.
So, a + a + 1 = 2005, so a = 1002 and b = 1002.
So, (1002, 1002, 1) is another solution.
If c ≥ 2, the exponent of a becomes very large, and since a ≥ 2, it is impossible for three numbers a, b, and c to add up to 2005.
Correctly solved by:
| 1. K.Sengupta | Calcutta, INDIA |
| 2. Davit Banana | Istanbul, Turkey |
| 3. Carlos de Armas | Barcelona City, Spain |
| 4. Seth Cohen | Concord, New Hampshire |
| 5. Rob Miles | Northbrook, Illinois |