An integer is written on each unit square of a 4×4 unit square chessboard.
The number in each unit square is equal to the sum of the numbers in all unit squares that share a common edge with that unit square.
What is the largest number of positive integers (out of the 16 numbers) that can be written on this chess board?

Solution to the Problem:
The most number of positive integers that can be placed on the chessboard is twelve.Here is one example:
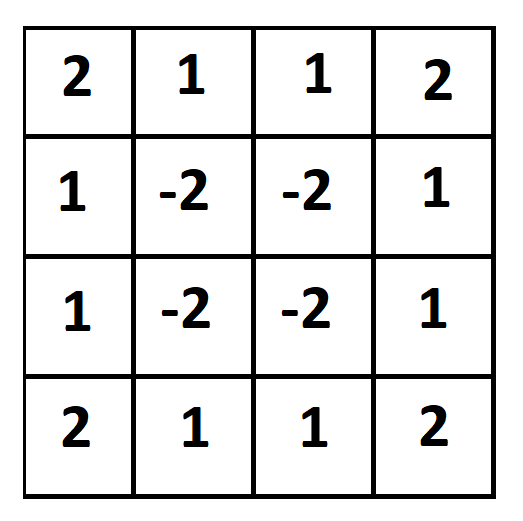
Kamal Lohia sent in a more general solution:
Let a and b be positive integers such that a > b, then only the four middle most integers are negatives as shown in the diagram.

Correctly solved by:
| 1. Kamal Lohia |
Holy Angel School, Hisar, Haryana, India |
| 2. K. Sengupta | Calcutta, India |