What is the ratio of the volumes of a regular tetrahedron and the smallest cube that can encompass it?
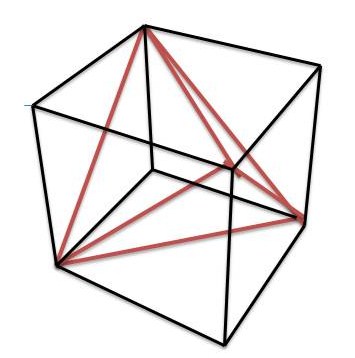
Solution:
The ratio is 1:3.
To find the ratio of the volumes of a regular tetrahedron and the smallest cube that can encompass it, we need to follow these steps:
1. Determine the volume of the regular tetrahedron.
2. Determine the side length of the smallest cube that can encompass the tetrahedron.
3. Calculate the volume of this cube.
4. Find the ratio of the volume of the tetrahedron to the volume of the cube.
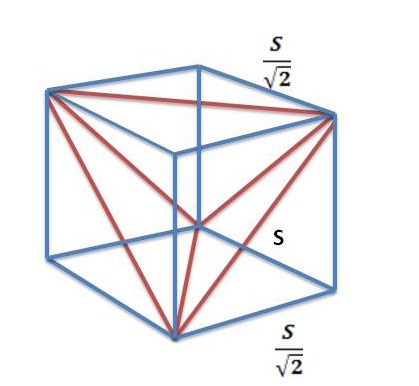
Let s = edge (side) of the terahedron.
Then the edge (side) of the cube is given by s / sqrt(2). (Use Pythagorean theorem on an isosceles right triangle).
The volume V of the cube with edge length s / sqrt(2) is given by the formula:
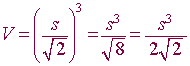
The volume V of a regular tetrahedron with edge length s is given by the formula:
V = (1/3) x (area of the base) x (height)
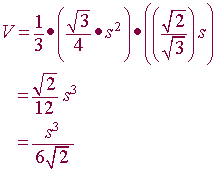
You can see that the ratio of the volume of the tetrahedron to the volume of the cube is 1/3.
Here is K. Sengupta's solution:
Choose three faces of a cube that meet at a vertex, and draw a diagonal across each face so that the lines all meet at the common vertex.
Now draw three lines to connect the other ends of these diagonals.
All six lines are the diagonal of a different face of the cube, so they are all equal in length, and therefore form the edges of a regular tetrahedron.
Thus the smallest cube that can encompass a tetrahedron with edges of length S is a cube with edges of length S/sqrt(2).
For such a tetrahedron, the base has an area
1/2 * B * H = 1/2 * S * S*sqrt(3)/2 = S^2*sqrt(3)/4
To find the height of the tetrahedron, we first find the distance of the centroid of the base from any edge of the base.
From symmetry, the centroid falls on the bisector of the three angles, and the distance of the centroid from an edge is S/(2*sqrt(3))
This distance and the height of the tetrahedron form the two legs of a right triangle whose hypoteneus is the height H of a triangular side, already found to be S*sqrt(3)/2.
From the Pythagorean theorem, the height x of the tetrahedron is
x = sqrt[(S*sqrt(3)/2)^2 - (S/(2*sqrt(3))^2]
x = S*sqrt(2/3)
The volume Vt of the tetrahedron is
Vt = 1/3 * B * H
Vt = 1/3 * S^2*sqrt(3)/4 * S*sqrt(2/3)
Vt = 1/3 * S^3/sqrt(8)
The volume Vc of the cube is
Vc = [S/sqrt(2)]^3
Vc = S^3/sqrt(8)
Thus the ratio of volumes of a regular tetrahedron and the smallest cube that can encompass it is 1:3.
Correctly solved by:
| 1. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 2. Kamal Lohia |
Holy Angel School, Hisar, Haryana, India |
| 3. Kelly Stubblefield | Mobile, Alabama, USA |
| 4. Dr. Hari Kishan |
D.N. College, Meerut, Uttar Pradesh, India |
| 5. Austin Hale | Grand Junction, Colorado, USA |
| 6. Davit Banana | Istanbul, Turkey |