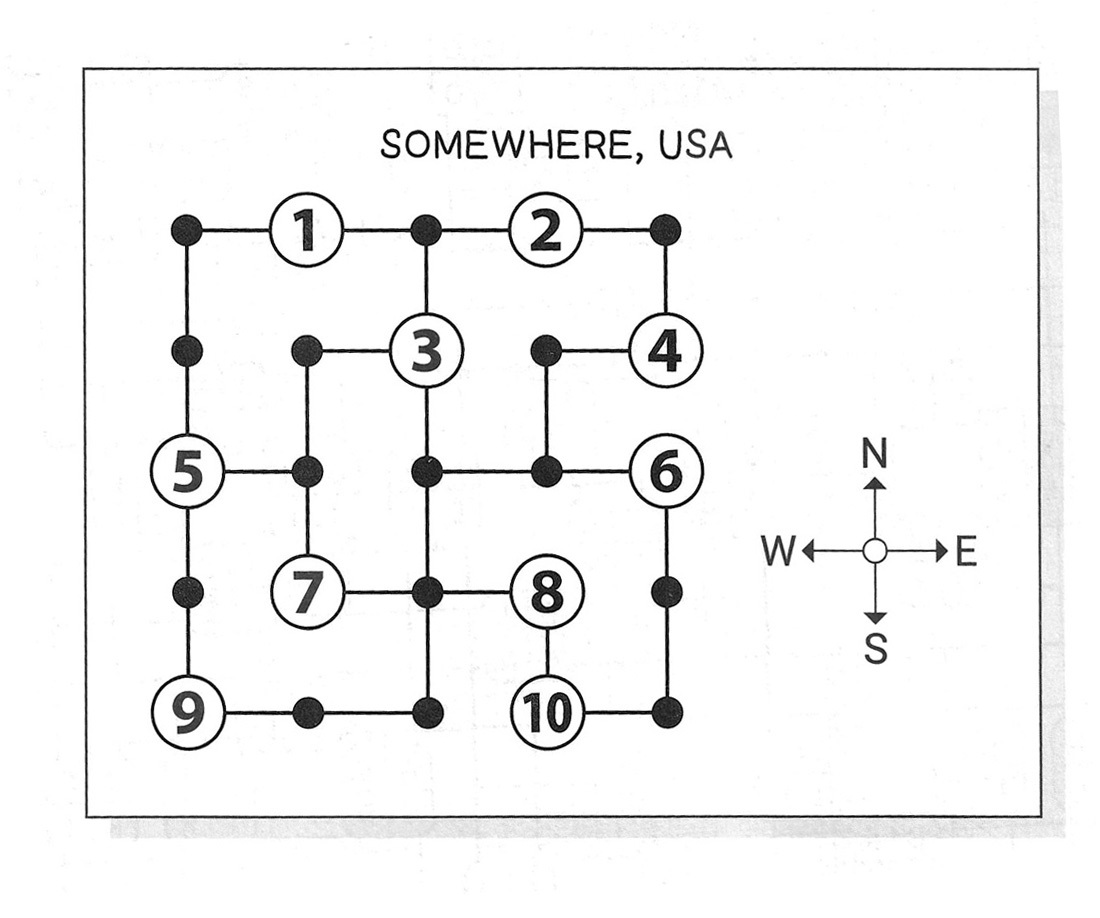
You are in a county, somewhere in the United States.
A local has given you a map of all the towns in this county.
Unfortunately, the map doesn’t have any place names.
Each numbered circle represents a town.
Using the map and the clues provided, can you figure out where each town is located?
CLUES:
1. It’s possible to take a trip starting at Alabaster and ending at Jubilee
that passes through every town without revisiting any point on the
map. The towns visited (in order) are:
Alabaster – Doppler – Foxtrot – Garamond – Ballyhoo – Hogshead – Edelweiss – Charity – Ides – Jubilee
2. The shortest path from Charity to Doppler requires moving both
north and south.
3. Ides is due south of Jubilee.
Click here for a printer version
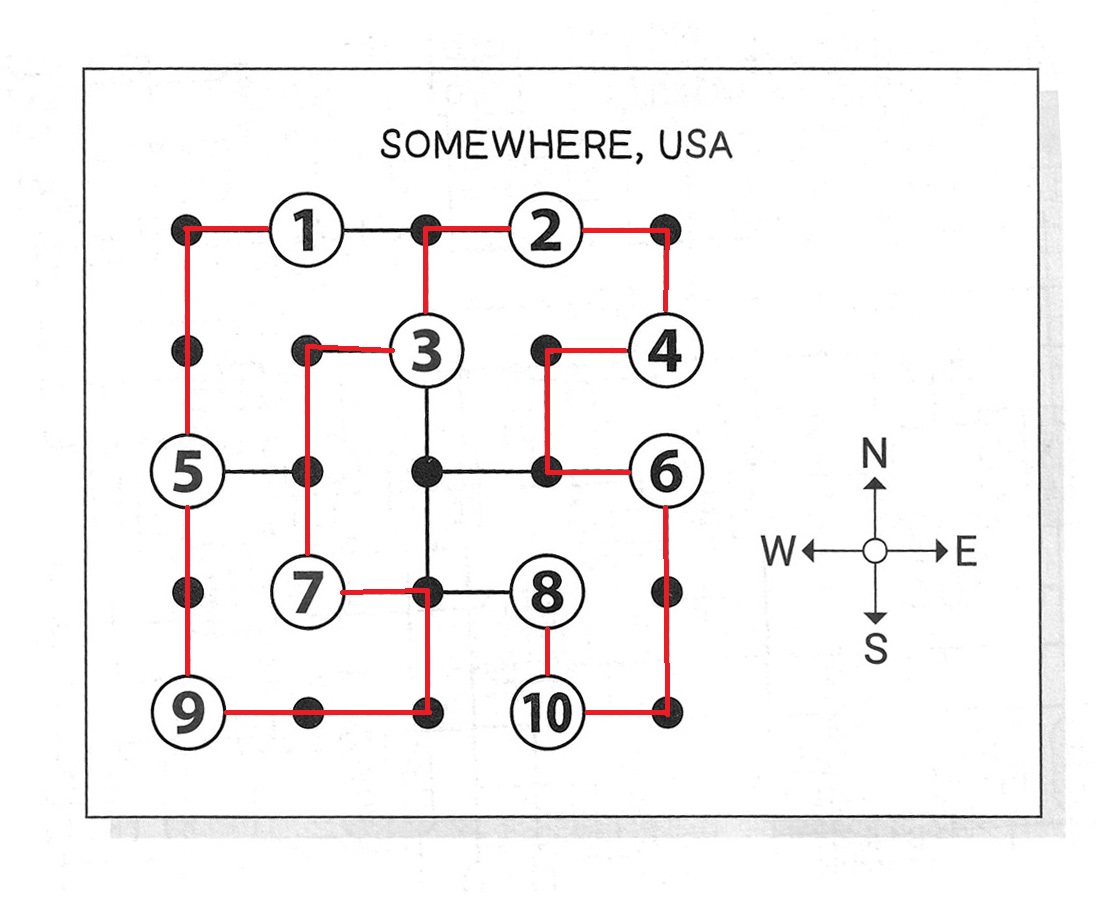
Solution:
The towns are:
1. Alabaster 2. Hogshead 3. Ballyhoo 4. Edleweiss 5. Doppler
6. Charity 7. Garamond 8. Jubilee 9. Foxtrot 10. Ides
First, I looked for a route that would pass through all ten towns and not retrace any point.
I could only find two such routes:
1 - 5 - 9 - 7 - 3 - 2 - 4 - 6 - 10 - 8 or its reverse:
8 - 10 - 6 - 4 - 2 - 3 - 7 - 9 - 5 - 1 and
1 - 5 - 9 - 8 - 10 - 6 - 4 - 2 - 3 - 7 or its reverse:
7 - 3 - 2 - 4 - 6 - 10 - 8 - 9 - 5 - 1
Clue 3 tells us that Ides is due south of Jubilee and clue 1 tells us that there are no towns between them.
The only pairs of numbers that meet this criteria are 9 and 5, 10 and 8, or 6 and 4.
Since we must end with Ides and Jubilee with no towns in between, it means that Ides is #10 and Jubilee is #8.
So, the route is: 1 - 5 - 9 - 7 - 3 - 2 - 4 - 6 - 10 - 8.
Now, you just need to match up the towns with the numbers to get:
Alabaster(1) – Doppler(5) – Foxtrot(9) – Garamond(7) – Ballyhoo(3) – Hogshead(2) – Edelweiss(4) – Charity(6) – Ides(10) – Jubilee(8).
I am not sure why clue #2 was needed, but it works in the solution:
The shortest path from Charity(6) to Doppler(5) is to go 2 blocks west, then 1 block south, then 1 block west to Garamond(7), then 1 block north, then 1 block west to Doppler(5).
Correctly solved by:
| 1. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 2. Dr. Hari Kishan |
D.N. College, Meerut, Uttar Pradesh, India |
| 3. Rod Fletcher | Tainan, Taiwan |