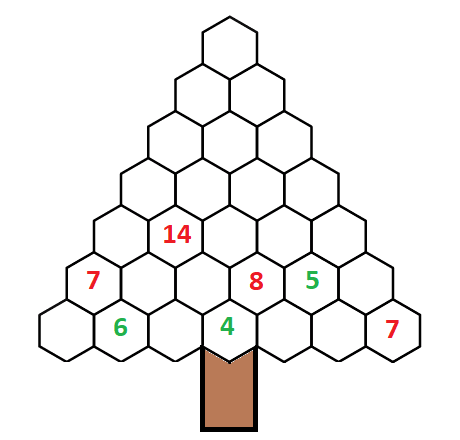
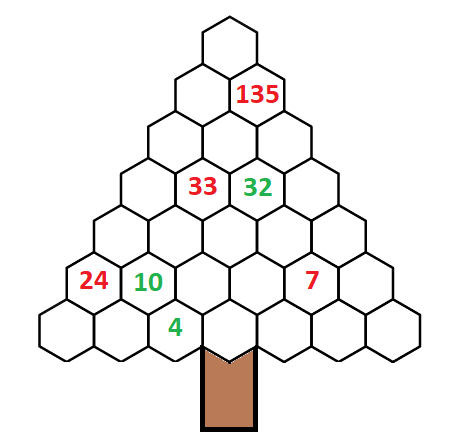
In each of the Christmas trees below, the number in each hexagon is the sum of the two numbers below it.
Can you fill in all the hexagons with the correct numbers?
Extra Credit: What is the relationship between the numbers at the very top of the two trees?
Click here for a Printer version
Solution to the Problem:
Here is an explanation:
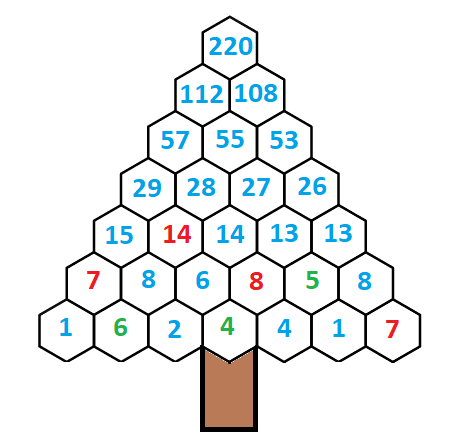
In the first tree, let w represent the number in the bottom row, 3rd hexagon over.
Let y and x represent the numbers in the hexagons above w.
Then you can set up three equations with the three unknowns:
6 + w = x
w + 4 = y
x + y = 14
So, 6 + w + 4 + w = 14
10 + 2w = 14
2w = 4
w = 2
Then y = 6 and x = 8
All the rest of the numbers can be obtained by adding or subtracting various cells.
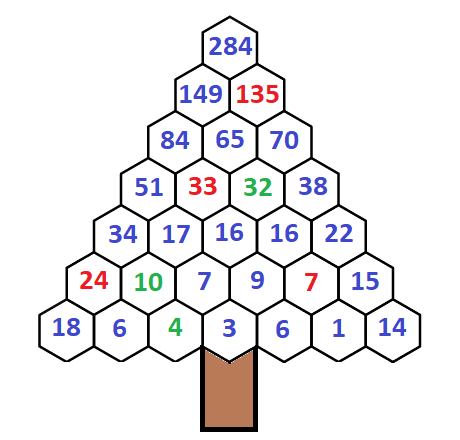
In the second tree, let a and b represent the numbers in the middle two hexagons in the second from the bottom row.
Then the three cells just above a and b would be represented by (10 + a), (a + b) and (b + 7).
You can then write two equations:
(a + b) + (10 + a) = 33 and
(7 + b) + (a + b) = 32
Then solving these equations gives you b = 9 and a = 7.
All the rest of the numbers can be obtained by adding or subtracting various cells.
For the extra credit, 220 and 284 are called amicable numbers.
Each is equal to the sum of the other's proper divisors (i.e., all the divisors except the number itself).
The proper divisors of 220 are: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, and 110, and they add up to 284.
The proper divisors of 284 are: 1, 2, 4, 71, and 142, and they add up to 220.
Correctly solved by:
| 1. Kamal Lohia ** |
Holy Angel School, Hisar, Haryana, India |
| 2. Dr. Hari Kishan ** |
D.N. College, Meerut, Uttar Pradesh, India |
| 3. Davit Banana ** | Istanbul, Turkey |
| 4. Dallan Cushing |
Mountain View High School, Mountain View, Wyoming, USA |
| 5. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 6. Mason Tims |
Mountain View High School, Mountain View, Wyoming, USA |
| 7. Kason Thompson |
Mountain View High School, Mountain View, Wyoming, USA |
| 8. Rich and Lynn Reifsnyder ** | Salisbury, Connecticut, USA |
| 9. Dave Randall and Logan Randall ** | Fort Collins, Colorado, USA |
| 10. Marco Morelli's 1ITE class ** |
Istituto Tecnico Tecnologico "G. e M. Montani", Fermo, Italy |
| 11. Ivy Joseph ** | Pune, Maharashtra, India |
| 12. Ben Harding |
University of Arizona, Tucson, Arizona, USA |
| 13. Kelly Stubblefield ** | Mobile, Alabama, USA |
** solved the extra credit