You are given a circle and will select n points on it.
You will then draw all the segments connecting all pairs of these points.
No three segments are allowed to intersect at a common point.
You must then determine the number of regions formed by these segments.
For example, if n = 2, you would draw one segment, and there would be two regions.
If n = 3, you would draw 3 segments, and the number of regions would be four.
In this problem, what is the number of regions formed if n = 6?
(No second chances on this problem)
Solution to the Problem:
The answer is 31 regions.
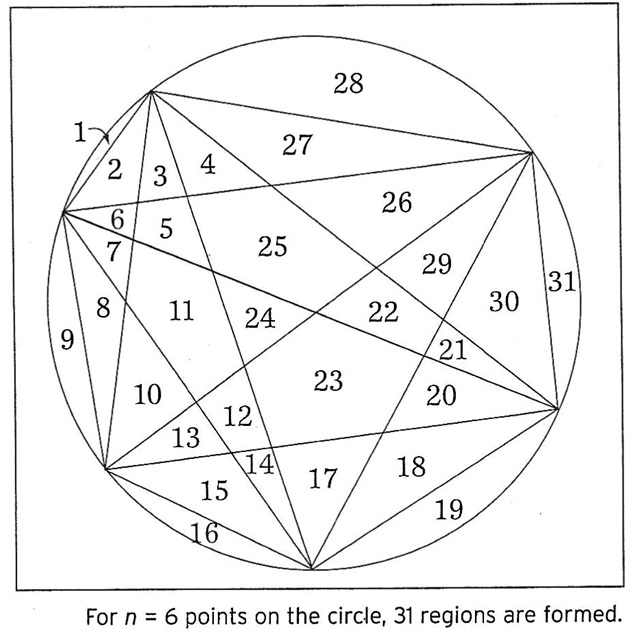
At first, I thought the answer would be 32 because of the pattern:
n = 1: regions = 1
n = 2: regions = 2
n = 3: regions = 4
n = 4: regions = 8
n = 5: regions = 16
But as you can see in the diagram above, the most number of regions that you can get when n = 6 is 31.
Colin Bowey gets extra credit for sending in the following:
Using the below formular you can calculate the number regions for any given value of n.
regions = 1/24 × (n^4 - 6n^3 + 23n^2 - 18n + 24)
n = 2 regions = 2
n = 3 regions = 4
n = 4 regions = 8
n = 5 regions = 16
n = 6 regions = 31
n = 7 regions = 57
n = 8 regions = 99
n = 9 regions = 163
n = 10 regions = 256
n = 11 regions = 386
n = 12 regions = 562
Correctly solved by:
| 1. Kamal Lohia |
Holy Angel School, Hisar, Haryana, India |
| 2. Dr. Hari Kishan |
D.N. College, Meerut, Uttar Pradesh, India |
| 3. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 4. Marco Morelli's 1ITE class |
Istituto Tecnico Tecnologico "G. e M. Montani", Fermo, Italy |
| 5. Ivy Joseph | Pune, Maharashtra, India |
| 6. Kelly Stubblefield | Mobile, Alabama, USA |