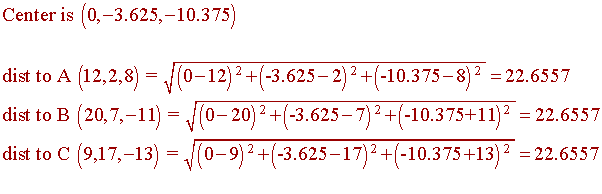Solution: I solved this problem in two different ways, and came up with two different answers, so I accepted both of them.
The center of the cube is (10.5, 9.5, -2.5) or
The center of the cube is (0, -3.625, -10.375).
METHOD #1:
Use the distance formula in three-space to determine the lengths of AB, AC, and BC.
Here is the distance formula in three space:
d = √ ( (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2 )
AC = 25.98
AB = 21.2132
BC = 15
Since we have determined three different lengths, they must represent an edge, the diagonal of a face, and the space diagonal.
Clearly, the longest, AC, is the space diagonal,
the next longest, AB, is the diagonal of a face, and
the shortest, BC, is the length of an edge.
So, I used the midpoint formula for the vertices of AC to find the center of the cube: (10.5, 9.5, -2.5)
The distance from A, B, and C from the center is 12.99 in each case.
METHOD #2:
The center must be equidistant from the three given vertices.
Let (x, y, z) represent the vertices of the center.
Use the distance formula to determine the distances from the center to each of the three points and then set them equal to each other and solve for x, y, and z.
Here is the distance formula in three space:
d = √ ( (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2 )
The distance from the center to point A:

The distance from the center to point B:
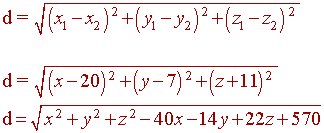
The distance from the center to point C:

Now set the distance to A and the distance to B equal and square each side:

Now set the distance to A and the distance to C equal and square each side:

Now set the distance to B and the distance to C equal and square each side:
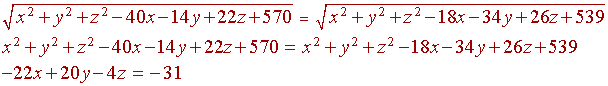
Now solve these three equations simultaneously to obtain (x, y, z):

Now check to see if the distance from the center to each point is the same: