Solve the following equation for P, I, and E, where PIE is a 3-digit number and the three digits are unique:
(Give both answers)
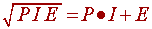
Solution:
PIE = 256 or 361
Here is Kamal Lohia's solution:
There are 22 3-digit perfect squares from 10² to 31². Now checking the numbers with 3 different digits, we get
13 = √169 ≠ 1•6 + 9
14 = √196 ≠ 1•9 + 6
16 = √256 = 2•5 + 6 👍🏻
17 = √289 ≠ 2•8 + 9
18 = √324 ≠ 3•2 + 4
19 = √361 = 3•6 + 1 👍🏻
23 = √529 ≠ 5•2 + 9
24 = √576 ≠ 5•7 + 6
25 = √625 ≠ 6•2 + 5
27 = √729 ≠ 7•2 + 9
28 = √784 ≠ 7•8 + 4
29 = √841 ≠ 8•4 + 1
31 = √961 ≠ 9•6 + 1
So, there are exactly two possible values of PIE: 256 & 361
Correctly solved by:
| 1. Kamal Lohia | Hisar, Haryana, India |
| 2. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 3. Davit Banana | Istanbul, Turkey |
| 4. Ivy Joseph | Pune, Maharashtra, India |
| 5. Dr. Hari Kishan |
D.N. College, Meerut, Uttar Pradesh, India |
| 6. Seth Cohen | Concord, New Hampshire, USA |
| 7. Eric Erdman |
Northrop High School, Fort Wayne, Indiana, USA |
| 8. Arda Karahan |
Trabzon Science High School, Trabzon Province, Turkey |
| 9. Kelly Stubblefield | Mobile, Alabama, USA |