Solve the following equation for P, I, and E, where PIE is a 3-digit number and the three digits are unique:
(Give both answers)
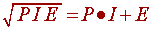
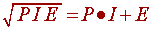
| 1. Kamal Lohia | Hisar, Haryana, India |
| 2. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 3. Davit Banana | Istanbul, Turkey |
| 4. Ivy Joseph | Pune, Maharashtra, India |
| 5. Dr. Hari Kishan |
D.N. College, Meerut, Uttar Pradesh, India |
| 6. Seth Cohen | Concord, New Hampshire, USA |
| 7. Eric Erdman |
Northrop High School, Fort Wayne, Indiana, USA |
| 8. Arda Karahan |
Trabzon Science High School, Trabzon Province, Turkey |
| 9. Kelly Stubblefield | Mobile, Alabama, USA |