Rod Fletcher sent the following to me about coloring maps made up of only rectangles:
How many colors are required to color a map consisting of only rectangular regions?
Contrary to the usual map coloring rules, let us add the requirement that even two regions that are touching at a corner must have different colors. The Four Color Theorem does not apply because its rules imply that the map can be represented as a planar graph, while the rule described above can result in graphs that are non-planar. Indeed, the argument below shows that some maps consisting of rectangular regions require five colors. However, this does not imply that five colors are sufficient, but only that five colors are necessary.
By definition, four squares touching at a point require four colors.

We proceed by assuming that only four colors are needed for any map.
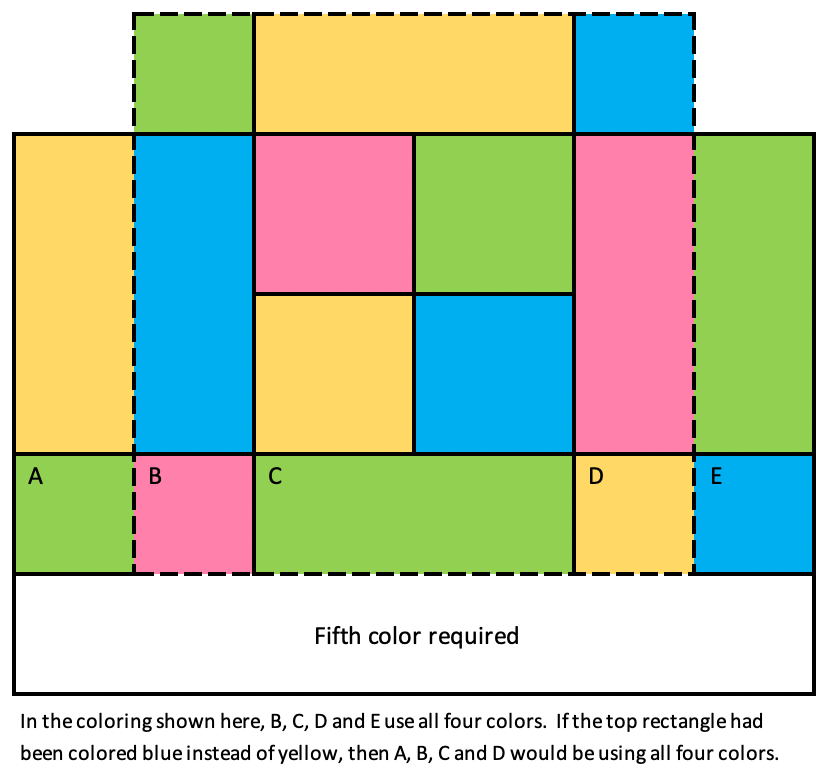
Let the four squares be surrounded by eight regions as shown below. Once a color is chosen for any side (i.e., a rectangle lying between two corner squares), then the colors for the three remaining sides are uniquely determined. After the sides are colored, the colors for the corner squares are determined.


Each side of the whole square now presents three different colors. Let two more regions be added to both the left and right sides as shown below. The two longer rectangles are each touching three different colors, so their colors are thus determined. Next, the colors of the two corner squares (A and E) are determined. Finally, any region that touches all five regions on the bottom (A through E) will be touching all four colors. Hence, a fifth color is needed for that region, which contradicts the initial assumption. QED.
Anyone who is motivated to tackle this problem might start by reading Wikipedia's article on 1-planar graphs. The graph corresponding to a map with rectangular regions, per the rules described above, is 1-planar. However, it happens to be a special case of a 1-planar graph that is not addressed in that article. The article does, however, state that 6 colors are sufficient for the general 1-planar graph, so if the answer to the present question is not 5, then it must be 6.