1. Football
If an ellipse is rotated about the major axis,
you obtain a football.

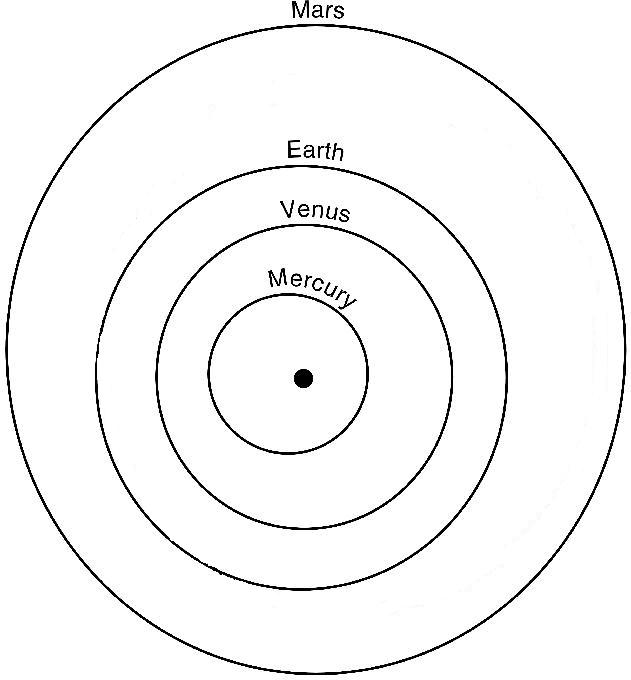
2. Satellite and Planet Orbits
Kepler's first law of planetary motion is:
The path of each planet is an ellipse with the sun at one focus.

3. Whispering Galleries -- in the old House of representatives
Statuary Hall in the U.S. Capital building is elliptic.
It was in this room that John Quincy Adams, while a member of the
House of Representatives, discovered this acoustical phenomenon.
He situated his desk at a focal point of the elliptical ceiling,
easily eavesdropping on the private conversations of other House
members located near the other focal point.

4. Whispering Galleries -- Mormon tabernacle
The Mormon Tabernacle in Salt Lake City has an elliptical ceiling.
You can hear a pin drop from 175 feet away.
The Tabernacle is 250 feet long, 150 feet wide, and 80 feet high.
The organ has 11,623 pipes!




5. Elliptical Pool Table
The reflection property of the ellipse is useful in elliptical pool --
if you hit the ball so that it goes through one focus,
it will reflect off the ellipse and
go into the hole which is located at the other focus.

6. The Ellipse in D.C.
The Ellipse near the White House in Washington, DC is aptly named.

7. Carpentry -- Bookcases
When I built the three sets of bookcases in my basement,
I needed
a decorative board for the top. I choose to cut out ellipses.






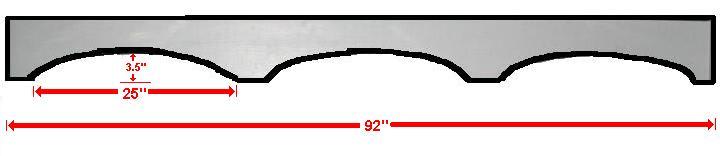
The dimensions of one of the boards is given above.
The 25" represents 2a , the fixed sum (and also the major axis).
The 3.5" represents b, half of the minor axis.
How did I determine c, the distance from the center to the focus?
Once I knew c, I placed thumb tacks at the two foci and used a piece
of string to draw the ellipse which was to be cut out.
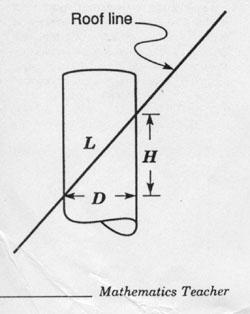
8. Carpentry -- Roof Vent Pipes
From a letter to the Mathematics Teacher
by William H. Enos
Recently a teacher asked if my class could provide him with a
set of ellipse templates that he could use for laying out holes in
roofs of varying pitches for standard 3 3/4-inch-outside-diameter
vent pipe. As my students were well acquainted with the string-
and-thumbtack constructions of ellipses, we accepted the challenge.
We knew that a roof of steeper pitch would call for an ellipse of
greater eccentricity. What we didn't count on was that the pitch
of the roof expressed as a ratio would jump right out at us from
our construction tables. To wit,