In a chess tournament, each contestant plays a match against every other contestant.
Each contestant gets 1 point for every match he wins, 0.5 points for every tied match, and 0 for every game he loses.
At the end of the tournament, it is seen that all competitors got a different number of points and the last competitor in the score ranking defeated each of the top three competitors.
Accordingly, what is the minimum number of competitors participating in the tournament?
Solution to the Problem:
There must be at least thirteen players in the tournament.Since the last player beat the top three players, he must have a total of three points (3 wins).
Each match results in ONE POINT ( a win/loss or 2 ties).
Use the combinations formula
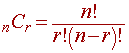to determine the number of points for n players taken r at a time).
Begin with the last person scoring 3 points, then add .5 points to each player in the standings.
For example with 4 players (the very minimum from the given info), there would be 3, 3.5, 4, and 4.5 points as the very minimum. This gives a total of 15 points but only 6 matches (and therefore 6 points) would be played. So, continue to compute each combination and check it with the minimum possible score. The first one to match is n = 13.
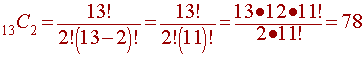so 13 contestants play 78 matches (and therefore get a total of 78 points).Here are the final scores for the thirteen players: 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9 and these add up to 78 points.
Each player has a different score and the last player beat the top three players so he has 3 points.
Below is a table showing all the calculations until I found the one that worked:
| Number of contestants |
Total # of matches (and Total POINTS) |
Smallest possible points |
|---|---|---|
| 4 | 6 | 3 + 3.5 + 4 + 4.5 = 15 (Not Possible because only 6 matches were played) |
| 5 | 10 | 3 + 3.5 + 4 + 4.5 + 5 = 20 (Not Possible because only 10 matches were played) |
| 6 | 15 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 = 25.5 (Not Possible because 15 < 25.5) |
| 7 | 21 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 + 6 = 31.5 (Not Possible because 21 < 31.5) |
| 8 | 28 | 3 + 3.5 + 4 + 4.5 + 5 + 5.5 + 6 + 6.5 = 38 (Not Possible because 28 < 38) |
| 9 | 36 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 = 45 (Not Possible because 36 < 45) |
| 10 | 45 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 = 52.5 (Not Possible because 45 < 52.5) |
| 11 | 55 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 = 60.5 (Not Possible because 55 < 60.5) |
| 12 | 66 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 +8.5 = 69 (Not Possible because 66 < 69) |
| 13 | 78 | 3 +3.5 +4 +4.5 +5 +5.5 +6 +6.5 +7 +7.5 +8 +8.5 +9 = 78 (Possible because 78 = 78) |
Colin Bowey sent in the final standings of the participants:
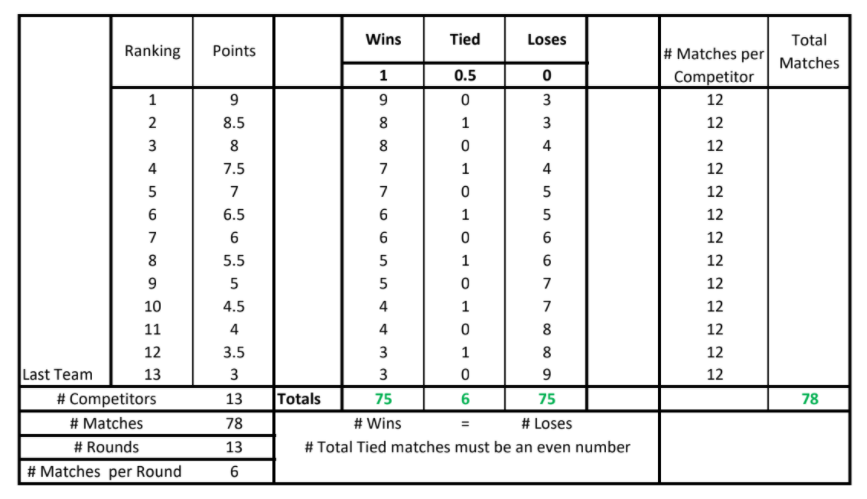
Veena Mg sent in an algebraic solution:
It is a Round Robin format.
If 'n' is number of teams,
number of matches played will be
= n *( n - 1) /2 - - - - - - - (A)
The team who stood last, defeated the first 3 teams. That means, the last team has scored at least 3 points.
For all the teams to have scored different points, there should at least be a minimum difference of 0.5. That means the scores are in an AP with a common difference of 0.5, and starting with 3
Total score of all teams, can at max be equal to number of games played.
The sum of AP is given by formula =
(n/2) * ( 2a + (n-1) *d)) - - - - (B)
a = 3, d = CD = 0.5
(A) should be greater than or equal to (B)
To find minimum number of competitors, equate both of them.
n * (n - 1) /2 = (n/2) * ( 2a + (n-1) *d))
n - 1 = (6 + (n-1)*0.5)
n = 6.5/0.5
n = 13.
So, a minimum of 13 competitors should play, to satisfy the given conditions..
Correctly solved by:
| 1. Colin (Yowie) Bowey | Beechworth, Victoria, Australia |
| 2. Veena Mg | Bangalore, Karnataka, India |
| 3. Kelly Stubblefield | Mobile, Alabama |